With the rise of multimodal Large Language Models (LLMs), the status of Vector Quantization (VQ) has also "risen with the tide." It serves as a tokenizer for vision and even arbitrary modalities, unifying multimodal data into an autoregressive generation framework. Unfortunately, since VQ-VAE was first proposed, its theoretical foundations have not seen significant progress. Issues such as codebook collapse or low utilization remain to be solved. Instead, alternative solutions like FSQ have been proposed, becoming strong "competitors" to VQ.
However, FSQ cannot replace VQ in all scenarios, so improvements to VQ itself remain valuable. Recently, I read the paper "Restructuring Vector Quantization with the Rotation Trick", which proposes a rotation trick claiming to improve a series of VQ-related issues. In this article, let us examine it together.
Review
As early as five years ago, in the blog post "A Brief Introduction to VQ-VAE: Quantized Autoencoders", we introduced VQ-VAE. Later, when introducing FSQ in "Embarrassingly Simple FSQ: ’Rounding’ Surpasses VQ-VAE", we revisited VQ-VAE in detail. Readers who are not yet familiar can read those two articles first.
Although VQ-VAE is named after VAE, it is actually an AE (Autoencoder) and lacks the generative capabilities of a VAE. The difference between it and a standard AE is that its encoding result is a discrete sequence rather than a continuous vector. That is, it can encode continuous or discrete data into a discrete sequence and allow the decoder to reconstruct the original input through this discrete sequence. This is much like a text tokenizer—converting input into another discrete sequence and then allowing the recovery of the original text through this sequence—which is why it is viewed as a tokenizer for arbitrary modalities.
In terms of formulas, a standard AE is: \begin{equation} z = \text{encoder}(x),\quad \hat{x}=\text{decoder}(z),\quad \mathcal{L}=\Vert x - \hat{x}\Vert^2 \end{equation} While VQ-VAE is: \begin{equation} \begin{aligned} z =&\, \text{encoder}(x)\\[5pt] z_q =&\, z + \text{sg}[q - z],\quad q = \mathop{\text{argmin}}_{e\in\{e_1,e_2,\cdots,e_K\}} \Vert z - e\Vert\\ \hat{x} =&\, \text{decoder}(z_q)\\[5pt] \mathcal{L} =&\, \Vert x - \hat{x}\Vert^2 + \beta\Vert q - \text{sg}[z]\Vert^2 + \gamma\Vert z - \text{sg}[q]\Vert^2 \end{aligned} \end{equation} Where "VQ" mainly refers to the process of transforming z to q, mapping z to one of e_1, e_2, \cdots, e_K. These e_i are called the Codebook and are also learnable vectors. The "masterstroke" of training VQ-VAE is the step z_q = z + \text{sg}[q - z], which is known as the "Straight-Through Estimator (STE)" for gradients.
STE
The Straight-Through Estimator appears because the transformation
from z to q involves a non-differentiable \text{argmin} operation, making it impossible
to propagate gradients directly to the encoder. In other words, the
encoder cannot be trained. To address this, VQ-VAE devised a trick: it
utilizes the stop_gradient operator and the
nearest-neighbor property of q and
z to replace q with z
during backpropagation, i.e., z_q = z +
\text{sg}[q - z].
At this point, in the forward pass, the \text{sg} is ignored, so z_q = z + q - z = q, meaning q is sent to the Decoder. During gradient calculation, the gradient of \text{sg} is zero, so \nabla z_q = \nabla z. Thus, the gradient can bypass the non-differentiable operator and reach the encoder directly; this is the "Straight-Through Estimator." However, while this allows the encoder to be optimized, the codebook cannot be. Therefore, VQ-VAE adds \beta\Vert q - \text{sg}[z]\Vert^2 to the loss function to optimize the codebook. Its intent is similar to K-Means, hoping that q becomes the center of all z for which it is the nearest neighbor. The final term \gamma\Vert z - \text{sg}[q]\Vert^2 encourages the encoder to actively cooperate to promote this clustering property.
From the perspective of the chain rule for gradients, we have: \begin{equation} \frac{\partial \mathcal{L}}{\partial z} = \frac{\partial q}{\partial z}\frac{\partial \mathcal{L}}{\partial q} \end{equation} Note that here z and q are vectors, so \frac{\partial \mathcal{L}}{\partial z} and \frac{\partial \mathcal{L}}{\partial q} are also vectors, while \frac{\partial q}{\partial z} is a matrix. Due to the non-differentiability from z to q, the problem is that \frac{\partial q}{\partial z} is not well-defined. STE essentially assumes \frac{\partial q}{\partial z}=I (the identity matrix), so \frac{\partial \mathcal{L}}{\partial z} = \frac{\partial \mathcal{L}}{\partial q}. This setting has a certain rationality, but is there room for improvement?
Intuitively, the result of STE is that for all z belonging to the same q, their gradients are the same \frac{\partial \mathcal{L}}{\partial q}, regardless of the distance between z and q. This seems to be an area for improvement: can we define a more general \frac{\partial q}{\partial z} that depends on the difference between z and q? To achieve this, we first generalize STE to: \begin{equation} z_q = \text{sg}[G]z + \text{sg}[q - Gz] \end{equation} where G is a matrix. Again, following the principle that \text{sg} is ignored in the forward pass and has zero gradient in the backward pass, we get z_q = q and \frac{\partial \mathcal{L}}{\partial z} = G^\top \frac{\partial \mathcal{L}}{\partial z_q}, which is equivalent to defining \frac{\partial q}{\partial z}=G.
Rotation
How should we choose G? The paper mentioned at the beginning proposes a reference scheme based on constructing G from the rotation transformation from z to q, which is the "Rotation Trick" in the title.
Specifically, the original paper considers the simple case where Gz = q, in which case \text{sg}[q - Gz] automatically becomes zero, simplifying to z_q = \text{sg}[G]z. To find the matrix G, we first normalize z and q into unit vectors \tilde{z} = \frac{z}{\Vert z\Vert} and \tilde{q} = \frac{q}{\Vert q\Vert}. Then we can construct a rotation transformation from \tilde{z} to \tilde{q}. We have previously explored the specific construction method in "The Orthogonal Matrix Transforming One Unit Vector to Another", and the answer is: \begin{equation} R = I + 2\tilde{q}\tilde{z}^{\top}- \frac{(\tilde{q} + \tilde{z})(\tilde{q} + \tilde{z})^{\top}}{1 + \cos\theta} = I + 2\tilde{q}\tilde{z}^{\top}- 2\left(\frac{\tilde{q} + \tilde{z}}{\Vert\tilde{q} + \tilde{z}\Vert}\right)\left(\frac{\tilde{q} + \tilde{z}}{\Vert\tilde{q} + \tilde{z}\Vert}\right)^{\top} \end{equation} where \theta is the angle between q and z. Using this result, we can write: \begin{equation} \tilde{q}=R\tilde{z}\quad\Rightarrow\quad q = \frac{\Vert q\Vert}{\Vert z\Vert} R z\quad\Rightarrow\quad G = \frac{\Vert q\Vert}{\Vert z\Vert} R \end{equation} To improve the efficiency of calculating Gz, we usually choose to use the associative property of matrix multiplication to first calculate \tilde{z}^{\top}z and \left(\frac{\tilde{q} + \tilde{z}}{\Vert\tilde{q} + \tilde{z}\Vert}\right)^{\top}z. However, note that we actually need \text{sg}[G]z, so we must stop the gradients of \tilde{q}, \tilde{z}, \frac{\Vert q\Vert}{\Vert z\Vert} before calculating Gz.
From a geometric perspective, \frac{\partial q}{\partial z}=G=\frac{\Vert q\Vert}{\Vert z\Vert} R makes the geometric relationship of \frac{\partial \mathcal{L}}{\partial q} relative to \frac{\partial \mathcal{L}}{\partial z} completely consistent with the geometric relationship of q relative to z. For example, the angle between \frac{\partial \mathcal{L}}{\partial q} and \frac{\partial \mathcal{L}}{\partial z} is equal to the angle between q and z, and the ratio of their magnitudes is also equal. These properties naturally possess a theoretical elegance, but can they truly improve the performance of VQ-VAE? Let us move to the experimental section.
Experiments
The paper compares the old STE and the rotation trick under the same configuration and finds that the performance of the rotation trick is "stunning":
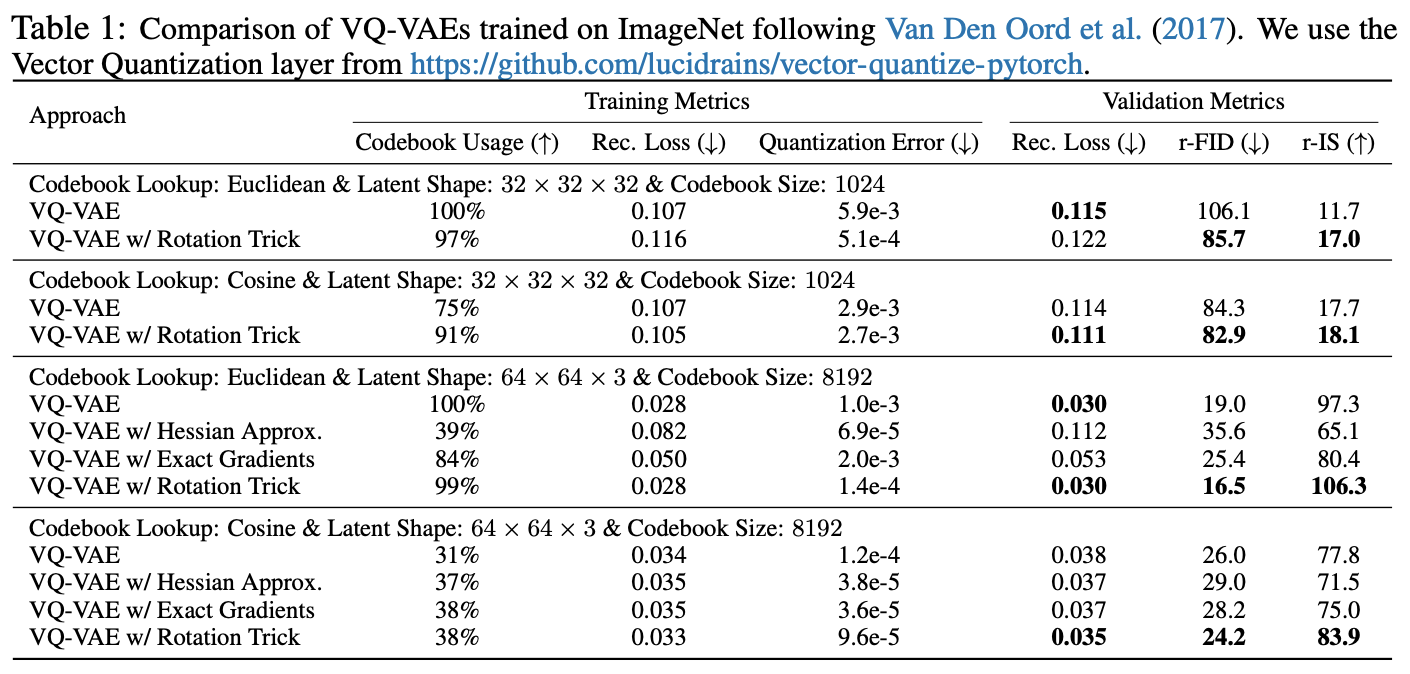
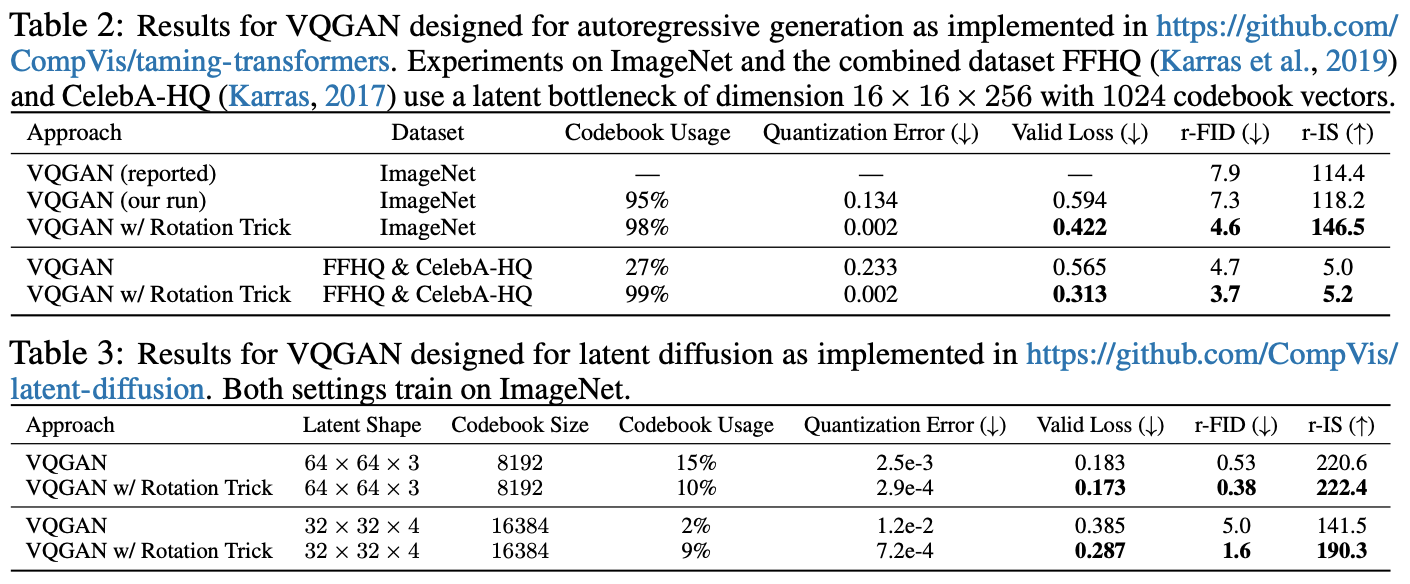
In short, metrics that should be high (codebook utilization, IS) are high, and metrics that should be low (reconstruction error, Loss, FID) are low, perfectly matching the characteristics of an ideal model. The code for the paper has also been open-sourced, and interested readers can try running it themselves.
Reflections
Does this mean that all VQ-VAE/VQ-GAN models can blindly adopt the rotation trick? When I added the rotation trick to my own previously working VQ-VAE code, I found that the performance actually became worse. Specifically, the reconstruction loss \Vert x - \hat{x}\Vert^2 became higher, while the codebook loss \Vert q - z\Vert^2 became lower.
After a brief analysis, I found that the problem lies in the choice of \frac{\partial q}{\partial z}=G=\frac{\Vert q\Vert}{\Vert z\Vert} R. The original STE is \frac{\partial q}{\partial z}=I. Here, the scale of the rotation matrix R is comparable to the identity matrix I, so the rotation trick introduces an extra factor of \frac{\Vert q\Vert}{\Vert z\Vert}. If \Vert q\Vert \ll \Vert z\Vert at initialization (which happened to be the case in my VQ-VAE implementation), then the gradient of the reconstruction loss under the rotation trick will be much smaller than under STE. Consequently, for the encoder, the gradient of the term \gamma\Vert z - \text{sg}[q]\Vert^2 becomes dominant.
In other words, the initial stage is equivalent to only optimizing \beta\Vert q - \text{sg}[z]\Vert^2 + \gamma\Vert z - \text{sg}[q]\Vert^2, which leads to q, z \to 0, i.e., codebook collapse. This explains the phenomenon of decreased codebook loss and increased reconstruction loss. Therefore, switching from STE to the rotation trick likely requires re-tuning \gamma at the very least. I briefly looked at the paper’s open-source code, and it seems they use K-Means on the initial encoder outputs to initialize the codebook. This way, the magnitudes of \Vert q\Vert and \Vert z\Vert are not too far apart, allowing for a smoother transition.
However, even after fine-tuning \gamma, I could not achieve better results with the rotation trick in my own VQ-VAE code. Thus, I remain cautious about the effectiveness of the rotation trick. Setting practice aside, I also struggle to understand the theoretical effectiveness of the rotation trick. The original paper’s analysis is that when q and z are very close, G is close to I, making \frac{\partial \mathcal{L}}{\partial z} \approx \frac{\partial \mathcal{L}}{\partial q} reasonable. When q and z are far apart—for example, when z is near the boundary of category q—the difference between G and I is large, meaning \frac{\partial \mathcal{L}}{\partial z} deviates significantly from \frac{\partial \mathcal{L}}{\partial q}. This causes z to "fly around," helping it break out of its "cage" and move toward new categories, thereby increasing codebook utilization. Obviously, this explanation feels somewhat unconvincing.
Furthermore, the rotation trick has another issue: it establishes a privileged central position—the origin. It is not hard to understand that the VQ operation itself is similar to K-Means clustering, and K-Means is centerless; it possesses translation invariance. Rotation, however, requires a center (the origin). Thus, the rotation trick is actually somewhat contrary to the original intent of VQ. Of course, VQ can be modified to find the nearest neighbor based on cosine similarity, which fits the rotation trick better, but this does not explain why the rotation trick also helps VQ based on Euclidean distance. Overall, the fundamental reason why the rotation trick works remains a question worth pondering.
Finally, some readers might wonder: since VQ has so many problems, why study VQ at all? Why not use the simpler FSQ? I believe that alternatives like FSQ cannot replace VQ in all scenarios. For instance, in Transformer-VQ introduced in "VQ the Key, and Transformer Complexity Becomes Linear", it is difficult to replace VQ with FSQ because VQ is applied at every layer. This distribution means the VQ model is very small, and FSQ tests show it only outperforms VQ when the model is sufficiently large.
Summary
The rotation trick is a new technique for training VQ (Vector Quantization) models recently proposed on arXiv. It generalizes the original Straight-Through Estimator (STE) and claims to improve issues such as codebook collapse or low utilization. This article provided a brief introduction to it and presented some of my thoughts and questions regarding its mechanism.
When reposting, please include the original article address: https://kexue.fm/archives/10489
For more detailed reposting matters, please refer to: "Scientific Space FAQ"