Another VQ Trick: Adding a Linear Transformation to the Codebook

Basics

Since we have introduced VQ and VQ-VAE multiple times in articles like "A Concise Introduction to VQ-VAE: Quantized Autoencoders" and "Embarrassingly Simple FSQ: ’Rounding’ Surpasses VQ-VAE", we will not repeat the details here. Instead, we directly provide the mathematical forms of a standard AE and VQ-VAE:

\begin{align} \text{AE:}&\qquad z = \text{encoder}(x),\quad \hat{x}=\text{decoder}(z),\quad \mathcal{L}=\Vert x - \hat{x}\Vert^2 \\[12pt] \text{VQ-VAE:}&\qquad\left\{\begin{aligned} z =&\, \text{encoder}(x)\\[5pt] z_q =&\, z + \text{sg}[q - z],\quad q = \mathop{\text{argmin}}_{e\in\{e_1,e_2,\cdots,e_K\}} \Vert z - e\Vert\\ \hat{x} =&\, \text{decoder}(z_q)\\[5pt] \mathcal{L} =&\, \Vert x - \hat{x}\Vert^2 + \beta\Vert q - \text{sg}[z]\Vert^2 + \gamma\Vert z - \text{sg}[q]\Vert^2 \end{aligned}\right.\label{eq:vqvae} \end{align}

To reiterate a common point: VQ-VAE is not a VAE; it is simply an AE with VQ added, lacking the generative capabilities of a VAE. VQ is the operation of mapping any vector to its nearest neighbor in a codebook. This operation is inherently non-differentiable, so STE is used to design gradients for the encoder, and two additional loss terms, \beta and \gamma, are added to provide gradients for the codebook while also regularizing the encoder’s representation.

Modification

The paper refers to its proposed method as SimVQ, though it does not explain what "Sim" stands for. I suspect "Sim" is an abbreviation for "Simple," because the modification in SimVQ is indeed very simple:

\begin{equation} \text{SimVQ-VAE:}\qquad\left\{\begin{aligned} z =&\, \text{encoder}(x)\\[5pt] z_q =&\, z + \text{sg}[q\color{red}{W} - z],\quad q = \mathop{\text{argmin}}_{e\in\{e_1,e_2,\cdots,e_K\}} \Vert z - e\color{red}{W}\Vert\\ \hat{x} =&\, \text{decoder}(z_q)\\[5pt] \mathcal{L} =&\, \Vert x - \hat{x}\Vert^2 + \beta\Vert q\color{red}{W} - \text{sg}[z]\Vert^2 + \gamma\Vert z - \text{sg}[q\color{red}{W}]\Vert^2\end{aligned}\right. \end{equation}

That’s right—it just multiplies the codebook by a matrix W, leaving everything else unchanged.

If you were originally training VQ using Equation [eq:vqvae], SimVQ can be applied directly. If you were using EMA (Exponential Moving Average) to update the codebook (i.e., \beta=0, with a separate moving average process to update the codebook, as done in VQ-VAE-2 and subsequent models—which is mathematically equivalent to using SGD to optimize the codebook loss while using other optimizers like Adam for other losses), you would need to disable that and reintroduce the \beta term for end-to-end optimization.

Some readers might immediately question: isn’t this just changing the codebook parameterization from E to EW? Since EW can be merged into a single matrix, it is equivalent to a new E. Theoretically, shouldn’t the model’s capacity remain unchanged? Yes, SimVQ does not change the model’s theoretical capacity, but it does change the optimization dynamics for SGD or Adam. It alters the optimizer’s learning process, thereby affecting the quality of the learned results.

Experiments

Before further reflection and analysis, let’s look at the experimental results of SimVQ. SimVQ was tested on vision and audio tasks. Table 1 is particularly representative:

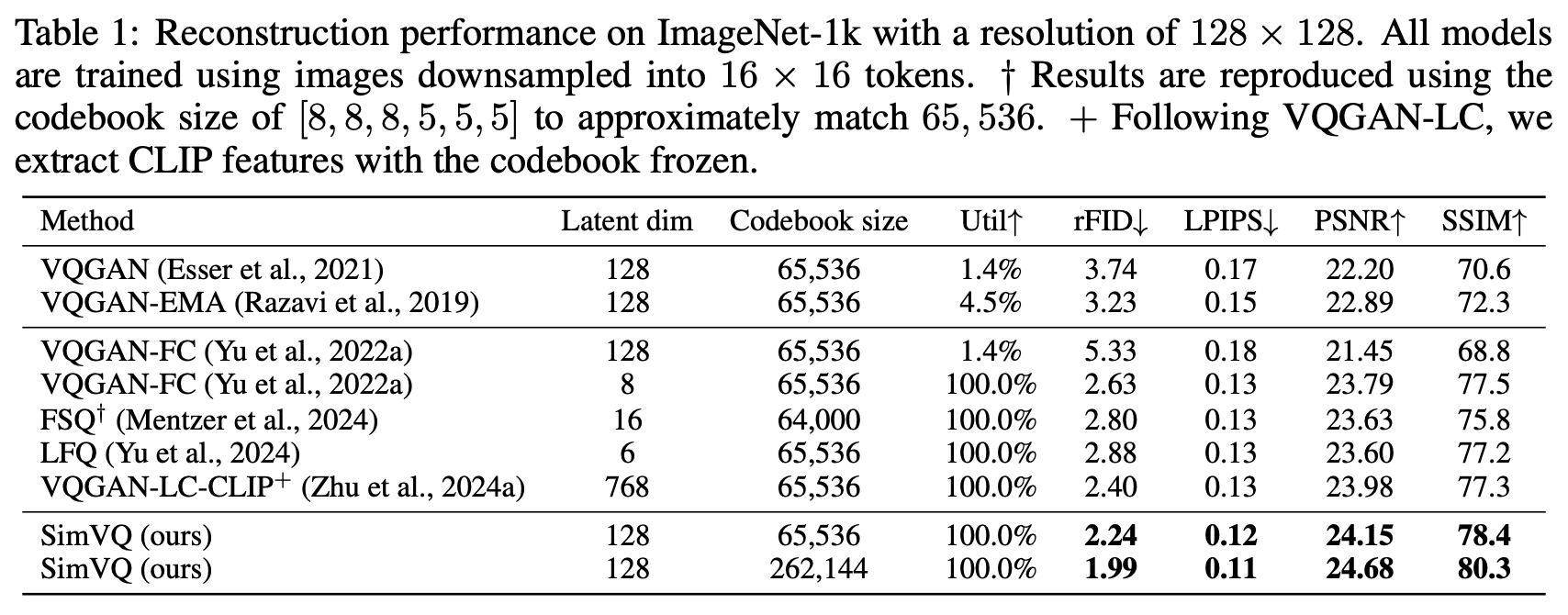
According to the paper, the SimVQ code was modified from the VQGAN code in the first row. The only change was inserting a linear transformation into the VQ layer. The improvement was significant: it not only achieved optimal reconstruction quality at the same codebook size but also allowed for further improvements by increasing the codebook size. This demonstrates the charm of SimVQ—simple and effective.

I also tried this on my own VQ-VAE code. Empirical tests showed that adding this linear transformation significantly accelerated the convergence of VQ-VAE and reduced the final reconstruction loss. I also experimented with a variant where W is a diagonal matrix, which is equivalent to element-wise multiplication of each code vector by a parameter vector (initialized to all ones). The results showed that this variant also had a similar effect, falling somewhere between standard VQ and SimVQ.

Analysis

Intuitively, the update of the codebook in VQ is quite "isolated." For example, if a sample z is quantized to q, the gradient of this sample only affects q and not other vectors in the codebook. SimVQ is different; it updates not only q but also W. Geometrically, W acts as a basis for the codebook. Once W is updated, the entire codebook is updated. Thus, SimVQ makes the "coupling" of the entire codebook much closer, providing a better chance of finding a global optimum rather than getting stuck in "fragmented" local optima.

Why does SimVQ improve codebook utilization? This is also easy to understand. Again, using the interpretation of W as a codebook basis: if codebook utilization is too low, W would exhibit "anisotropy," meaning the basis would lean toward the codes that are being utilized. However, once the basis changes in this way, its linear combinations should also lean toward the utilized codes, preventing utilization from dropping too low. Simply put, a learnable basis automatically increases its own utilization, thereby raising the utilization of the entire codebook.

We can also describe this process mathematically. Assuming the optimizer is SGD, the update for code e_i in standard VQ is: \begin{equation} e_i^{(t+1)} = e_i^{(t)} - \eta\frac{\partial \mathcal{L}}{\partial e_i^{(t)}} \end{equation} If e_i is not selected in the current batch, \frac{\partial \mathcal{L}}{\partial e_i^{(t)}} is zero, and the code is not updated. However, if e_i is parameterized as q_i W, then: \begin{equation} \begin{aligned} q_i^{(t+1)} =&\, q_i^{(t)} - \eta\frac{\partial \mathcal{L}}{\partial q_i^{(t)}} = q_i^{(t)} - \eta \frac{\partial \mathcal{L}}{\partial e_i^{(t)}} W^{(t)}{}^{\top}\\ W^{(t+1)} =&\, W^{(t)} - \eta\frac{\partial \mathcal{L}}{\partial W^{(t)}} = W^{(t)} - \eta \sum_i q_i^{(t)}{}^{\top}\frac{\partial \mathcal{L}}{\partial e_i^{(t)}} \\ e_i^{(t+1)}=&\,q_i^{(t+1)}W^{(t+1)}\approx e_i^{(t)} - \eta\left(\frac{\partial \mathcal{L}}{\partial e_i^{(t)}} W^{(t)}{}^{\top}W^{(t)} + q_i^{(t)}\sum_i q_i^{(t)}{}^{\top}\frac{\partial \mathcal{L}}{\partial e_i^{(t)}}\right) \end{aligned} \end{equation} We can see that:

1. W is updated based on the sum of gradients of all selected codes, so it naturally leans toward high-utilization directions.

2. Due to the presence of q_i^{(t)}\sum_i q_i^{(t)}{}^{\top}\frac{\partial \mathcal{L}}{\partial e_i^{(t)}}, the update for code i is almost never zero, regardless of whether it was selected.

3. q_i^{(t)}\sum_i q_i^{(t)}{}^{\top}\frac{\partial \mathcal{L}}{\partial e_i^{(t)}} acts as a projection onto the high-utilization direction, pushing every code toward that direction.

However, too much of a good thing can be harmful. If all codes push too hard toward high-utilization directions, it might lead to codebook collapse. Therefore, SimVQ defaults to a conservative strategy: only update W, while all q vectors remain fixed after random initialization. This almost entirely eliminates the possibility of codebook collapse. Fortunately, experiments show that with appropriate code dimensions, updating both q and W performs similarly to updating only W, so readers can choose the form they prefer.

Extension

Setting aside the context of VQ, the practice of introducing extra parameters that are mathematically equivalent—meaning they don’t change the model’s theoretical fitting capacity but only change the optimization dynamics—is known as "Overparameterization."

Overparameterization is not uncommon in neural networks. For instance, the mainstream architecture now uses Pre-Norm, i.e., x + f(\text{RMSNorm}(x)). The \gamma vector multiplied at the end of RMSNorm is usually overparameterized because the first layer of f is typically a linear transformation (e.g., Attention projecting to Q, K, V, or FFN projecting to a higher dimension). During inference, the \gamma vector can be merged into the linear transformation of f, yet we rarely see the \gamma removed during training.

This is because many believe overparameterization plays an indispensable role in making deep learning models "easy to train." Removing overparameterization from well-validated models is risky. Here, "easy to train" refers to the fact that gradient descent—a method theoretically prone to local optima—somehow consistently finds solutions that perform well in practice. Works like "On the Optimization of Deep Networks: Implicit Acceleration by Overparameterization" suggest that overparameterization implicitly accelerates training, acting similarly to momentum in SGD.

Finally, since VQ can essentially be understood as a sparse training scheme, the insights and modifications brought by SimVQ might be applicable to other sparse training models, such as MoE (Mixture of Experts). In current MoE training schemes, updates between Experts are relatively independent; only the Experts selected by the Router have their parameters updated. Is it possible that, like SimVQ, adding a shared linear transformation after all Experts could improve Expert utilization? Of course, MoE has many differences from VQ, so this is just a conjecture.

Summary

This article introduced another training trick for VQ (Vector Quantization)—SimVQ. By simply adding a linear transformation to the VQ codebook without any other changes, one can achieve faster convergence, improved codebook utilization, and lower reconstruction loss. It is remarkably simple and effective.

Reprinting: Please include the original address of this article: https://kexue.fm/archives/10519

For more details on reprinting/citation, please refer to: "Scientific Space FAQ"