How to reduce the number of sampling steps while ensuring generation quality is a key issue at the application level of diffusion models. Among the early efforts, DDIM, introduced in "Generative Diffusion Models (Part 4): DDIM = High-level DDPM", was the first attempt at accelerating sampling. Later, works introduced in "Generative Diffusion Models (Part 5): SDE for General Framework" and "Generative Diffusion Models (Part 5): ODE for General Framework" linked diffusion models with SDEs and ODEs. Consequently, numerical integration techniques were directly applied to accelerate diffusion model sampling. Among these, ODE acceleration techniques are the most abundant due to their relative simplicity; we also introduced an example in "Generative Diffusion Models (Part 21): Accelerating ODE Sampling with the Mean Value Theorem".
In this article, we introduce another particularly simple and effective acceleration trick—Skip Tuning, from the paper "The Surprising Effectiveness of Skip-Tuning in Diffusion Sampling". To be precise, it is used in conjunction with existing acceleration techniques to further improve sampling quality. This means that while maintaining the same sampling quality, it can further compress the number of sampling steps, thereby achieving acceleration.
Model Review
Everything starts with U-Net, which is the mainstream architecture for current diffusion models. The later U-ViT also maintains roughly the same form, except it replaces the CNN-based ResBlocks with Attention-based ones.
U-Net originated from the paper "U-Net: Convolutional Networks for Biomedical Image Segmentation" and was originally designed for image segmentation. Its characteristic is that the input and output sizes are identical, which perfectly fits the modeling needs of diffusion models, so it was naturally migrated to the diffusion field. Structurally, U-Net is very similar to a conventional AutoEncoder, involving progressive downsampling followed by progressive upsampling, but it adds extra Skip Connections to solve the information bottleneck of the AutoEncoder:

Different papers may implement U-Net with variations in detail, but they all share the same Skip Connections. Roughly speaking, the output of the first layer (block) has a "shortcut" directly to the last layer, the output of the second layer has a "shortcut" to the second-to-last layer, and so on. These "shortcuts" are the Skip Connections. Without Skip Connections, due to the "barrel effect" (the law of the minimum), the information flow of the model would be limited by the feature map with the smallest resolution. For tasks that require complete information, such as reconstruction or denoising, this would result in blurry outputs.
In addition to avoiding information bottlenecks, Skip Connections also play a role in linear regularization. Obviously, if the layers near the output only use Skip Connections as input, it is equivalent to the subsequent layers being added for nothing; the model becomes closer to a shallow model or even a linear model. Therefore, the addition of Skip Connections encourages the model to prioritize using the simplest possible (i.e., closer to linear) prediction logic, using more complex logic only when necessary. This is one of the inductive biases.
Just a Few Lines
After understanding U-Net, Skip Tuning can actually be explained in just a few sentences. We know that the sampling of a diffusion model is a multi-step recursive process from \boldsymbol{x}_T to \boldsymbol{x}_0, which constitutes a complex non-linear mapping from \boldsymbol{x}_T to \boldsymbol{x}_0. For practical considerations, we always hope to reduce the number of sampling steps. Regardless of which specific acceleration technique is used, it ultimately reduces the non-linear capability of the entire sampling mapping.
The idea behind many algorithms, such as ReFlow, is to adjust the noise schedule so that the sampling process follows a path as "straight" as possible. This makes the sampling function itself as linear as possible, thereby reducing the quality degradation caused by acceleration techniques. Skip Tuning, on the other hand, thinks in reverse: Since acceleration techniques lose non-linear capability, can we compensate for it from elsewhere? The answer lies in Skip Connections. As we just mentioned, their presence encourages the model to simplify its prediction logic. If the Skip Connections are "heavier," the model is closer to a simple linear or even identity model. Conversely, by reducing the weight of the Skip Connections, we can increase the model’s non-linear capability.
Of course, this is just one way to increase the model’s non-linear capability, and there is no guarantee that the non-linearity it adds is exactly the non-linearity lost by sampling acceleration. However, the experimental results of Skip Tuning show a certain equivalence between the two! So, as the name suggests, by performing a certain amount of Tuning on the Skip Connection weights, one can further improve the sampling quality after acceleration, or reduce the number of sampling steps while maintaining sampling quality. The tuning method is simple: assuming there are k + 1 Skip Connections, we multiply the Skip Connection closest to the input layer by \rho_{\text{top}}, and the Skip Connection furthest from the input layer by \rho_{\text{bottom}}. The rest change uniformly according to depth. In most cases, we set \rho_{\text{top}}=1, so basically only the parameter \rho_{\text{bottom}} needs to be tuned.
The experimental results of Skip Tuning are quite impressive. Two tables are excerpted below; for more experimental result images, please refer to the original paper.
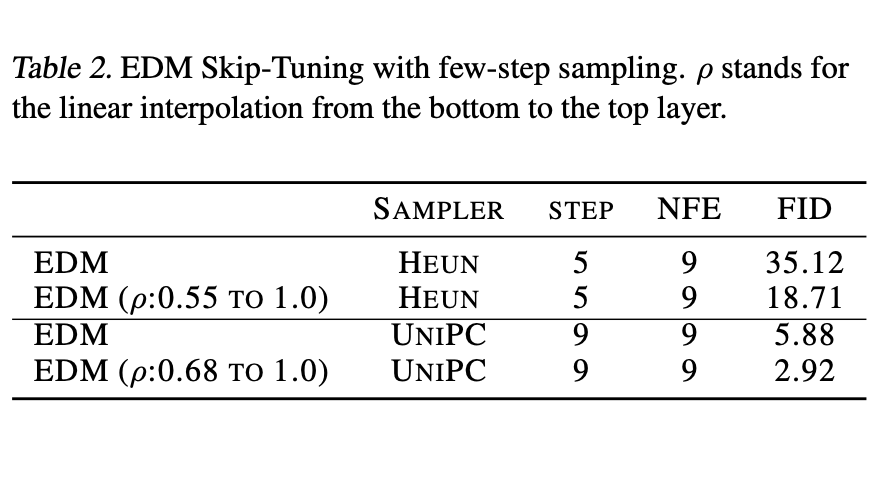
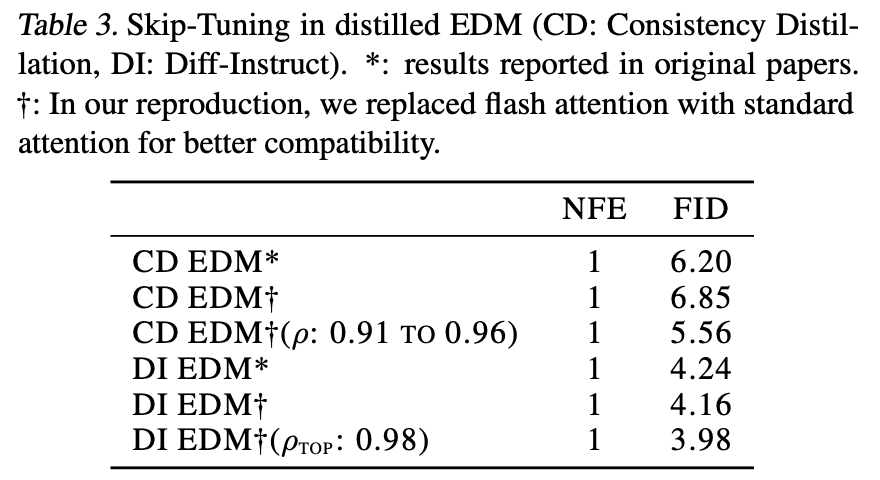
Personal Thinking
This is likely the simplest article in the diffusion series, without long passages or complex formulas. Readers could easily understand it by reading the original paper directly, but I am still willing to introduce it. Like the previous article "Generative Diffusion Models (Part 23): SNR and Large Image Generation (Part 2)", it reflects the author’s unique imagination and observation, something I feel I personally lack.
A paper closely related to Skip Tuning is "FreeU: Free Lunch in Diffusion U-Net". It analyzes the roles of different components of U-Net in diffusion models and finds that Skip Connections are mainly responsible for adding high-frequency details, while the backbone is mainly responsible for denoising. In this light, we can understand Skip Tuning from another perspective: Skip Tuning primarily experiments with ODE-based diffusion models. These models often show increased noise when sampling steps are reduced. Therefore, shrinking the Skip Connections relatively increases the weight of the backbone, enhancing the denoising capability—a case of "prescribing the right medicine." Conversely, for SDE-based diffusion models, one might need to reduce the shrinkage ratio of Skip Connections, or even increase their weight, because such models often produce over-smoothed results when sampling steps are reduced.
Skip Tuning adjusts Skip Connections, so does a model like DiT, which has no Skip Connections, have no chance of application? Not necessarily. Although DiT has no Skip Connections, it still has residuals. The design of the Identity branch is essentially an inductive bias for linear regularization. Therefore, even without Skip Connections, tuning the residuals might yield some gains.
Summary
This article introduced a technique that effectively improves the generation quality of diffusion models after accelerated sampling—reducing the weight of the "shortcuts" (Skip Connections) in the U-Net. The entire framework is very simple, clear, and intuitive, making it well worth learning.
Reprinting: Please include the original address of this article: https://kexue.fm/archives/10077
For more detailed reprinting matters, please refer to: "Scientific Space FAQ"